同じ電気の分野でも、技術では中2理科で学習する電流分野とは違う切り口で出題されることがあります。
今回は、理科では出題されないが、技術だと出題される知識を紹介します。
回路の違いと特徴を覚える
回路には、直列回路と並列回路があります。回路の違いと特徴を覚えましょう。
直列回路
下のような回路が直列回路です。
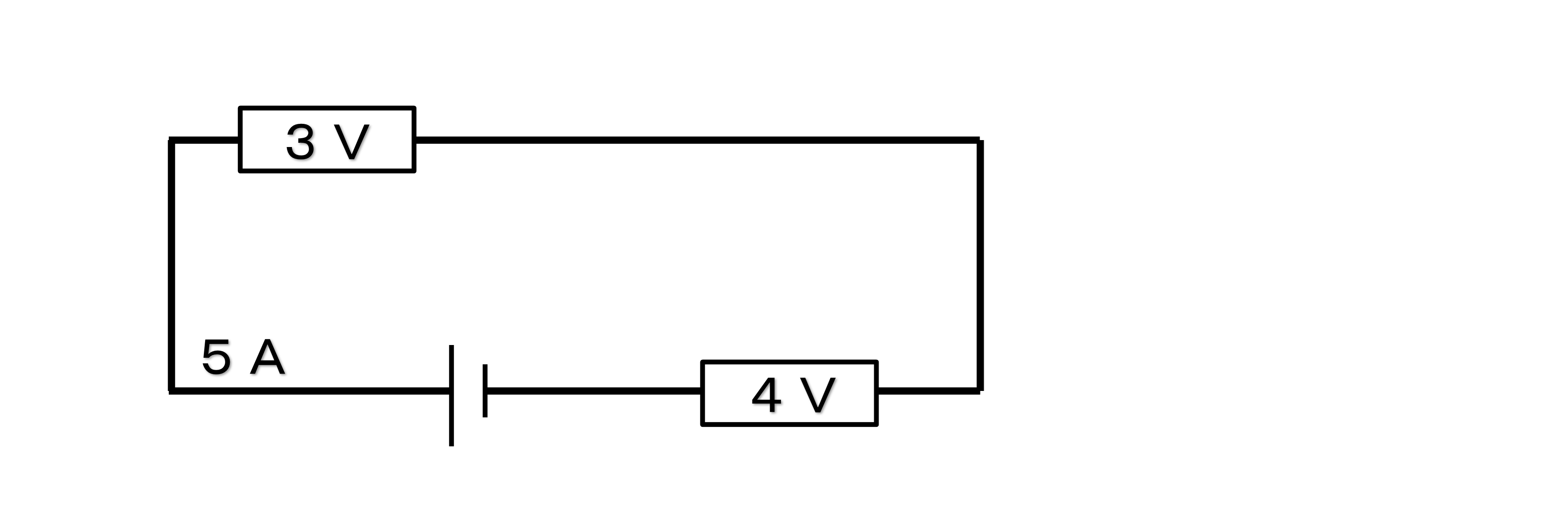
【図1】
ポイント
①回路図の+極から-極まで一本道の回路。回路図をなぞると一筆書きができるのが特徴
②電流は、回路の全ての部分で同じ
図1のとき、どこで計っても電流は、5A
③電圧は、全ての電圧の合計
図1のとき、回路全体の電圧は、7V(3V+4V)
並列回路
下の図のような回路が並列つなぎの回路です。
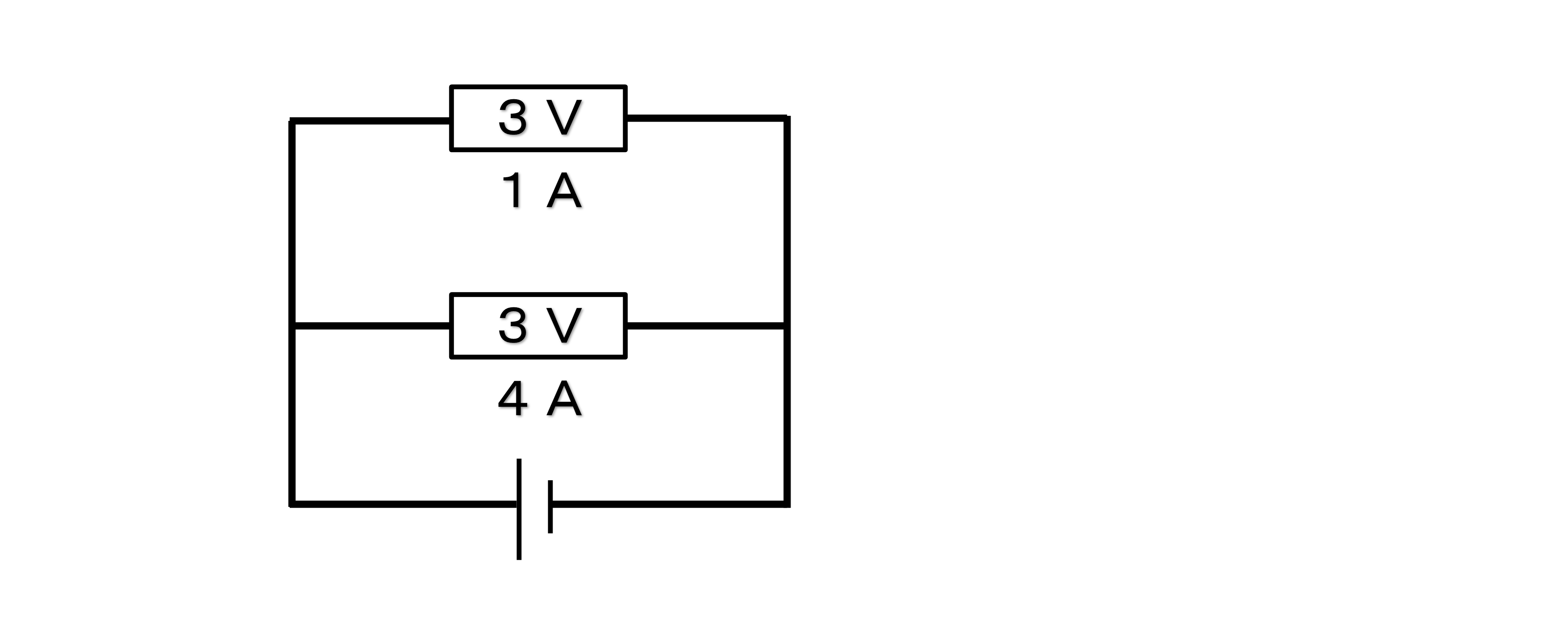
【図2】
ポイント
①回路図の+極から-極まで一本道の回路ではない。回路図をなぞると一筆書きができないのが特徴
②電流は、回路に流れる合計
図2のとき、回路全体の電流は、5A(1A+4A)
③電圧は、どこで計っても同じ
図2のとき、回路全体の電圧は、3V
では今紹介した知識を使って問題を解いてみてください。
【例題1】
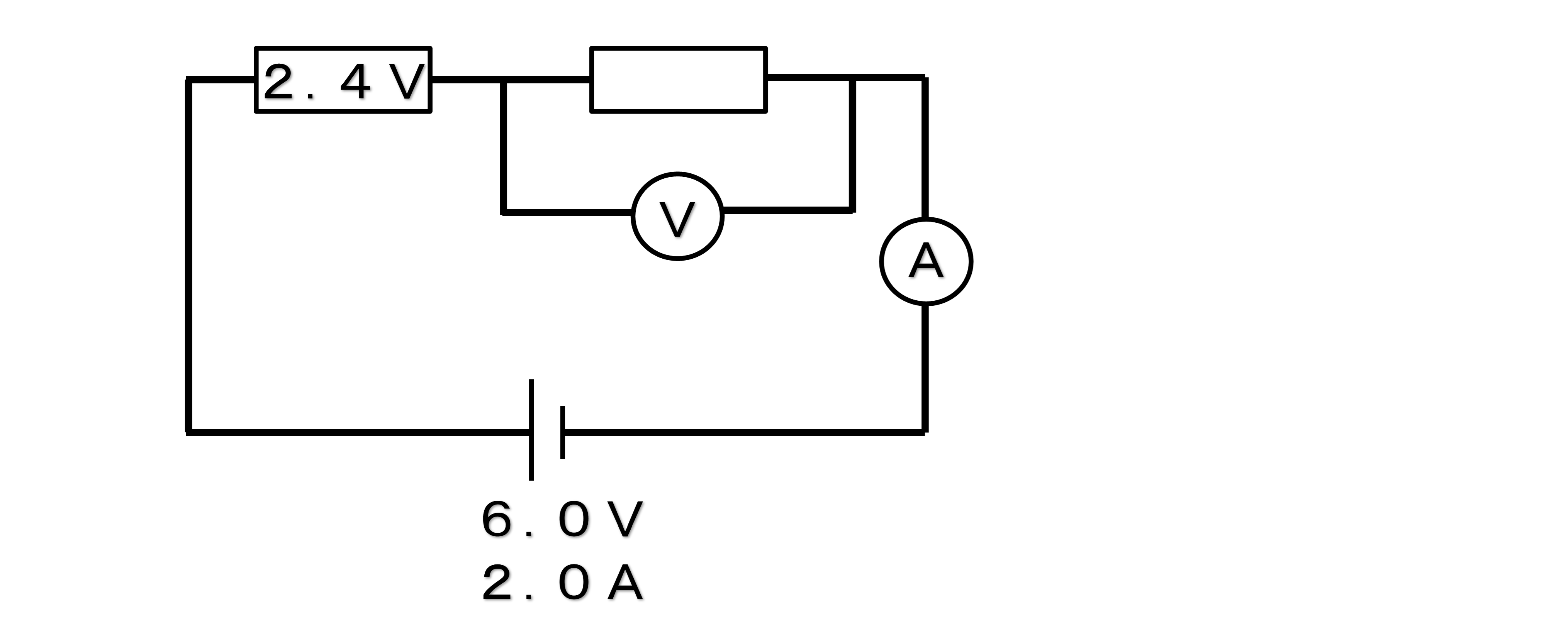
Q 以下の回路の電流計と電圧計の値を求めなさい
●解説
まずは、回路の種類を考えましょう。
一筆書きができるので直列回路です。
(電圧計は並列につなぎます。回路とは関係ないので無視してください。)
直列回路の場合、電流はどの地点でも同じです。
ですから、電流計の値は、2.0Aになります。
また、電圧の場合は、全ての電圧の合計です。
したがって、3.6V(6.0V-2.4V)
A.電流計2.0A ,電圧計3.6V
合成抵抗の求め方を覚える

合成抵抗(抵抗が1つではなく2つ以上ある回路)のときは、抵抗の出し方にもう一つ知識が必要になります。
抵抗が直列につながっていると並列につながっている場合で、抵抗を出すルールが変わります。
抵抗が直列につながっている場合
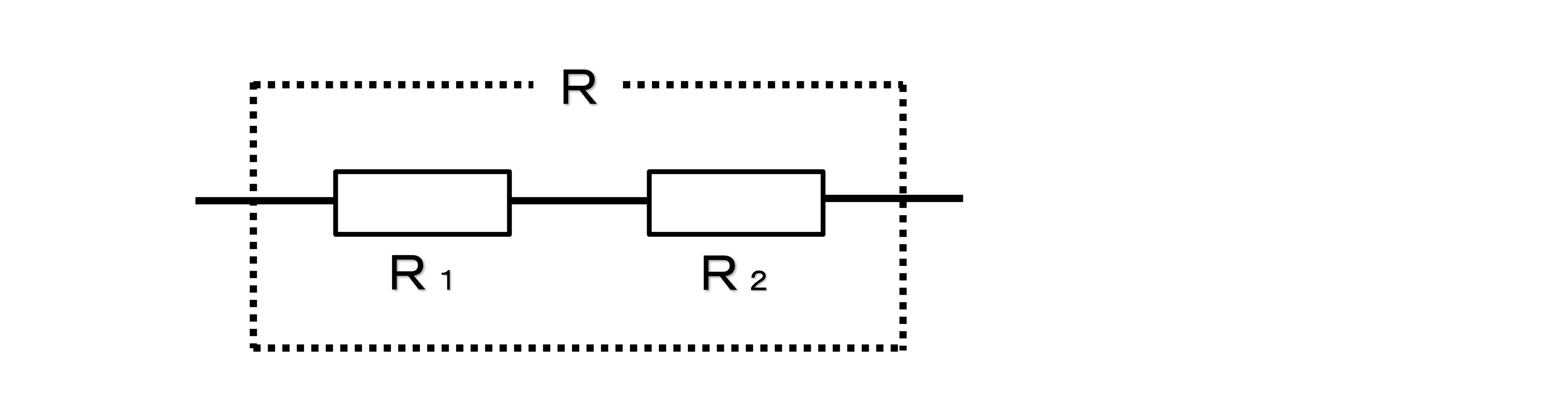
全体の抵抗は各抵抗の和になります。
R=R1+R2
抵抗が並列につながっている場合
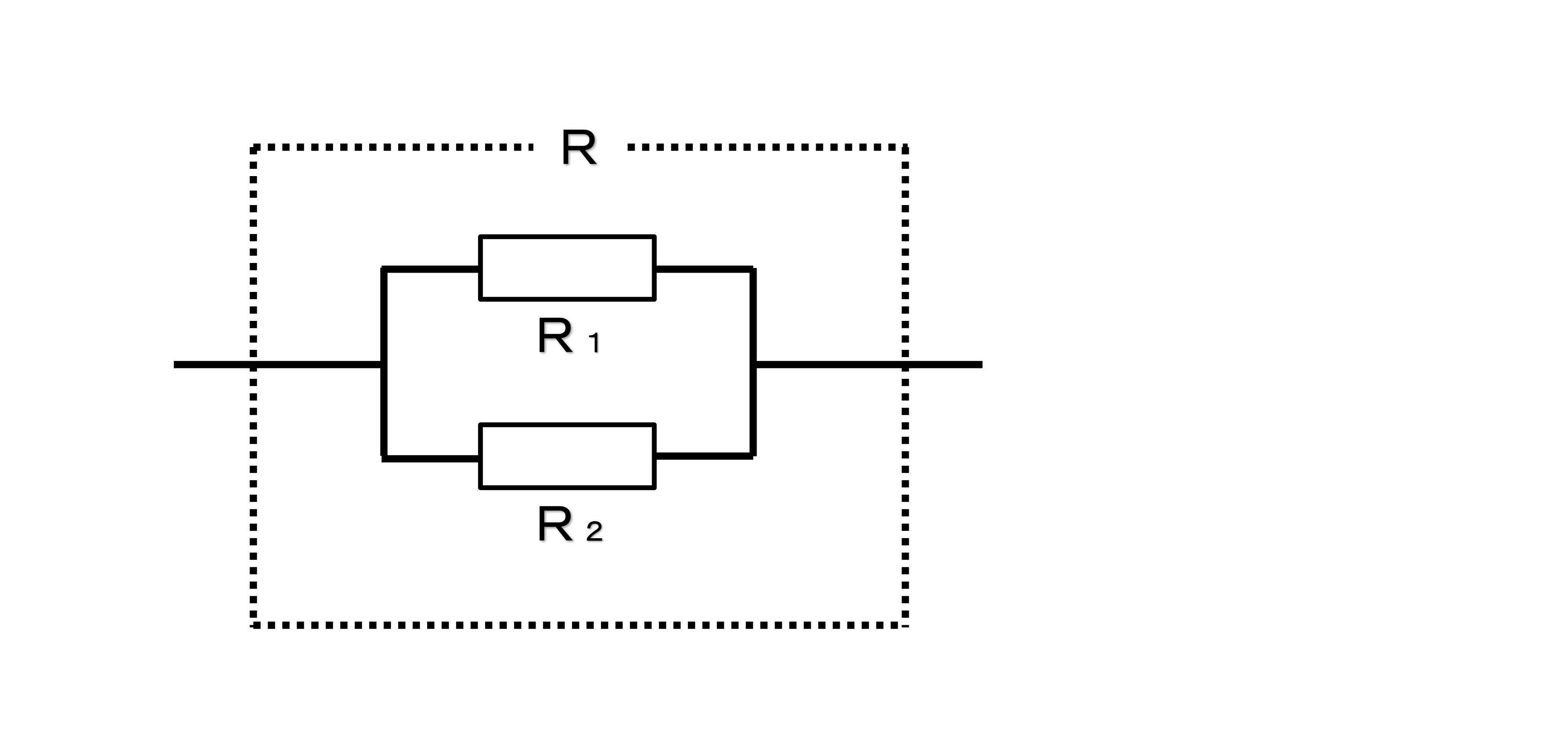
全体の抵抗は各抵抗の逆数の和をさらに逆数にしたものになります。
1/R1+1/R2=1/R ⇒R(1/Rを逆数にする)
【例題2】
Q 以下の回路図の全体の抵抗を求めなさい。
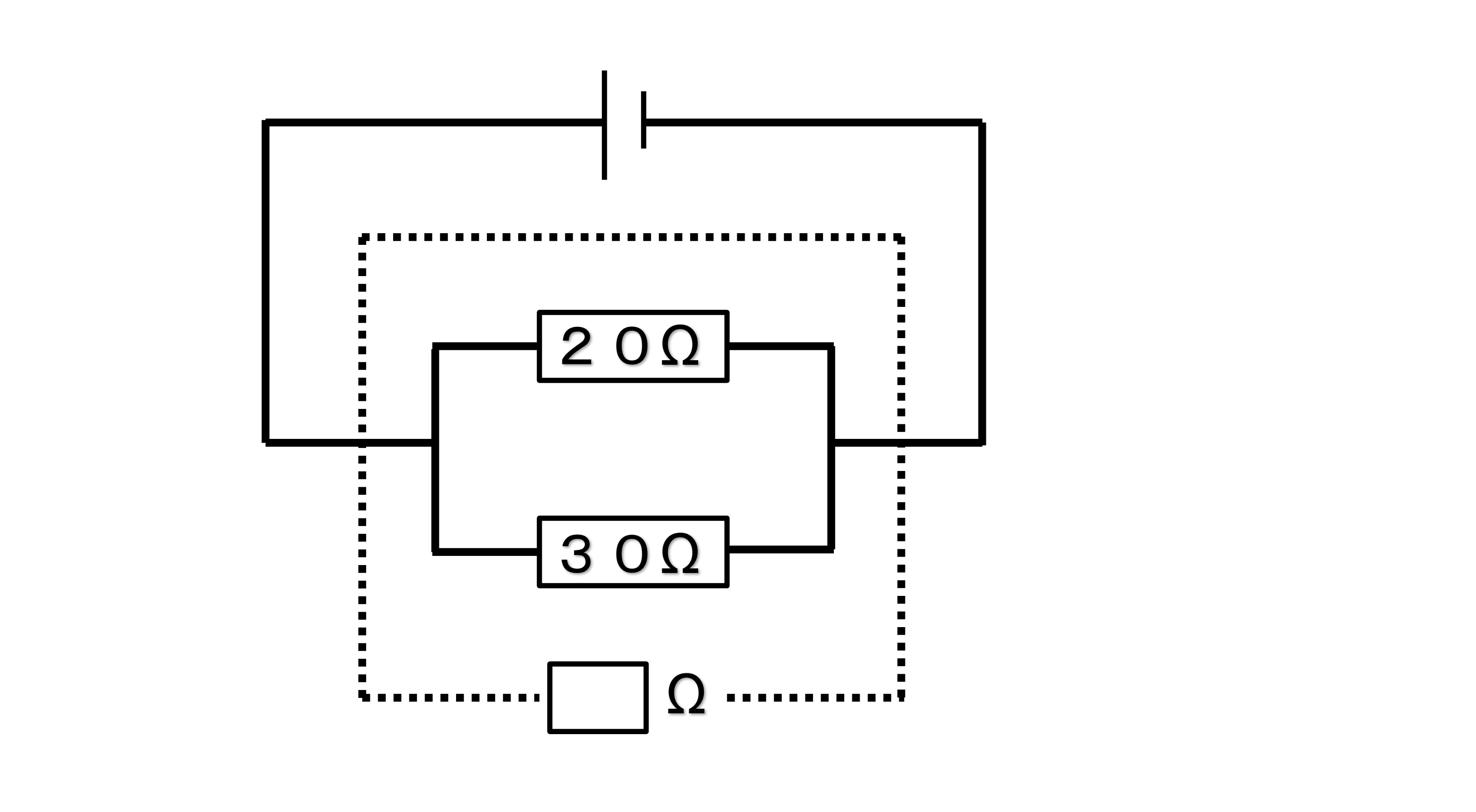
●解説
抵抗が、並列につながれています。
そこで抵抗が並列につながっている場合の公式を使います。
1/20+1/30=5/60=1/12 ⇒12(1/12の逆数)
A.12Ω
単位を覚える
あまり多くはないケースですが、実際に定期テストに出題されていたことがあるので紹介しておきます。
1KΩ=1000Ω
1A=1000㎃
この知識を使って、例題を解いてみてください。
【例題3】
Q(1)~(4)の空欄に当てはまる数字を答えなさい
(1)3kΩ=□Ω
(2)400Ω=□kΩ
(3)10A=□㎃
(4)150㎃=□A
●解答
(1)3000Ω (2)0.4kΩ (3)10,000㎃ (4)0.15A
合成抵抗の応用問題

【例題4】
Q 回路全体の合成抵抗を求めなさい
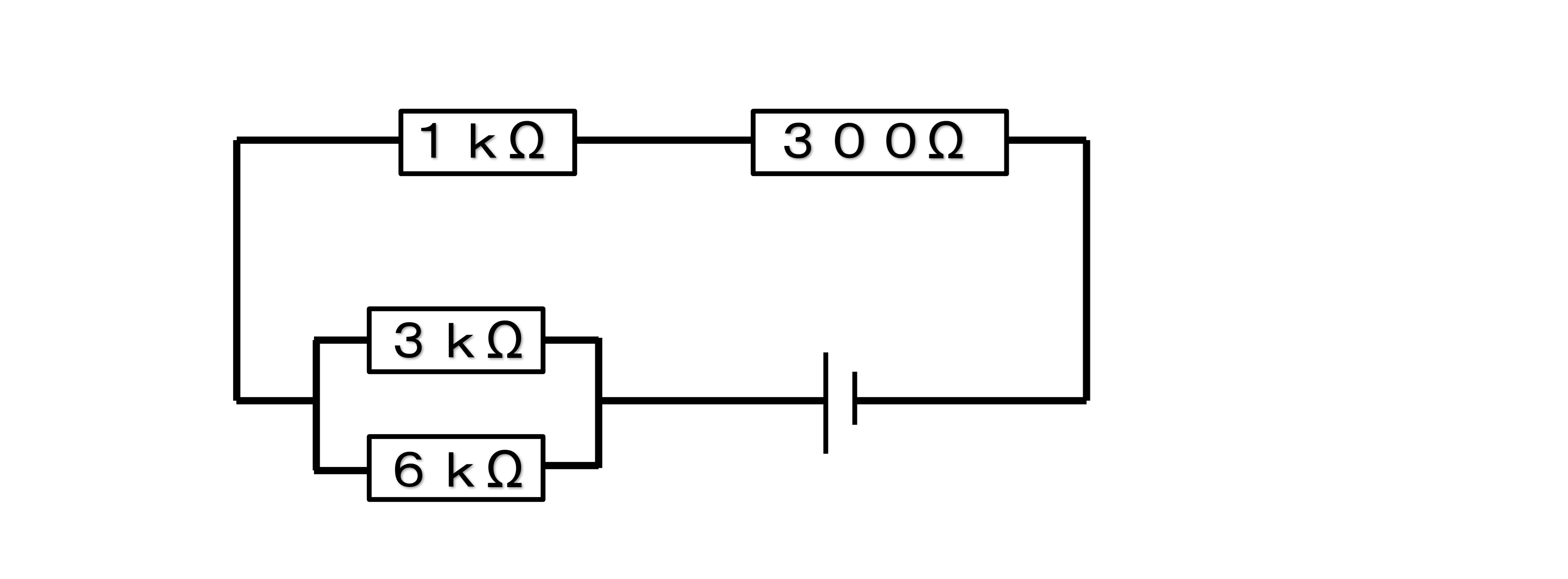
●解説
直列回路と並列回路が混ざっているときは、並列回路から考えます。
つまり、3kΩと6kΩの合成抵抗を求めます。
回路が並列つなぎのときの合成抵抗Rの求め方は、各抵抗の逆数の和をさらに逆数にしたものです。
実際に数字を入れると
1/3+1/6=2/6=1/2 ⇒2(1/2を逆数にします)
これで3kΩと6kΩの合成抵抗が2kΩです。つまり、下の図のように考えることができます。
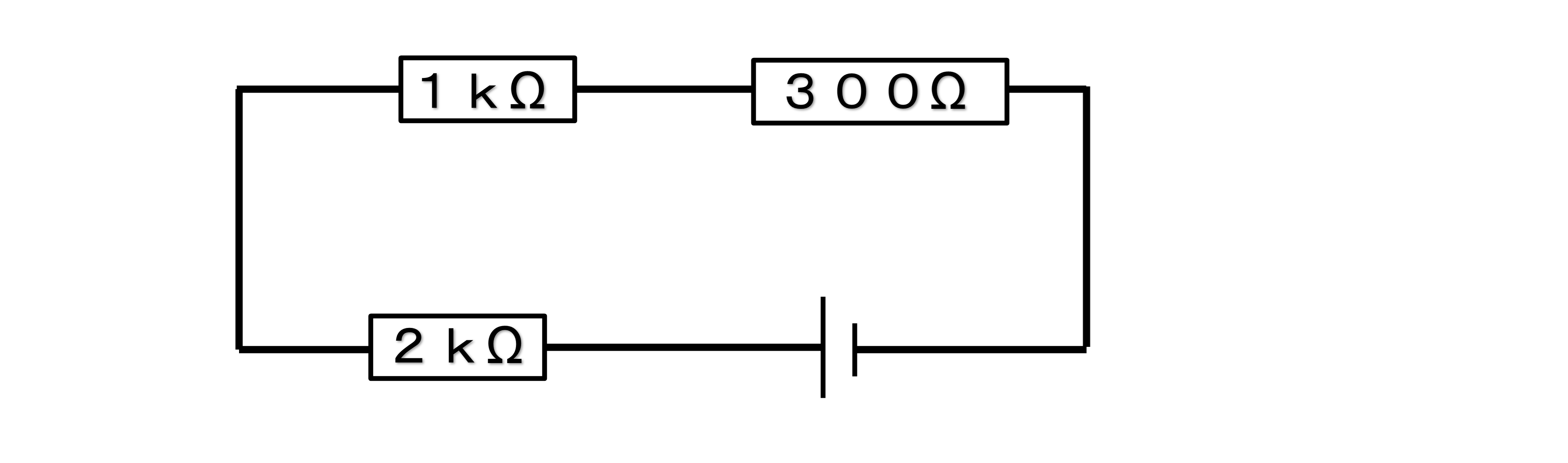
2kΩと1kΩと300Ωの抵抗が直列につながれていると同じ状況だとわかります。
抵抗が直列につながれている場合は、各抵抗の和で求めることができます。
2(kΩ)+1(kΩ)+300(Ω) ←単位を揃えます
=2(kΩ)+1(kΩ)+0.3(kΩ)
=2.3(kΩ)
A.2.3kΩ
では最後に例題が理解できたかの確認として、練習問題を解いてみてください。
【練習問題】
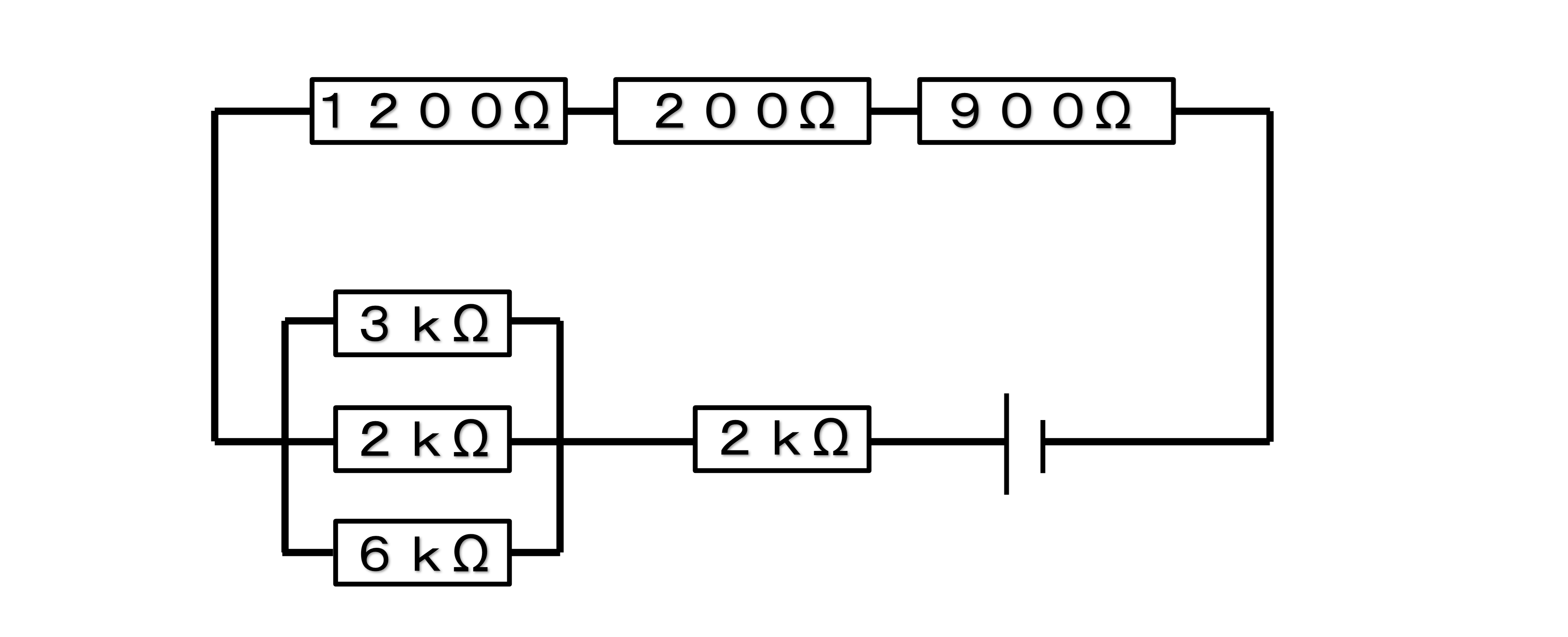
Q回路全体の合成抵抗を求めなさい
●解説
例題同様、直列回路と並列回路が混ざっているときは、並列回路から考えます。
この問題の場合は、3kΩ・2kΩ・6kΩの合成抵抗を求めます。
1/3+1/2+1/6 =6/6=1/1 ⇒1(1/1を逆数にします)
合成抵抗が1kΩだと分かりました。これで下の図のように考えることができます。
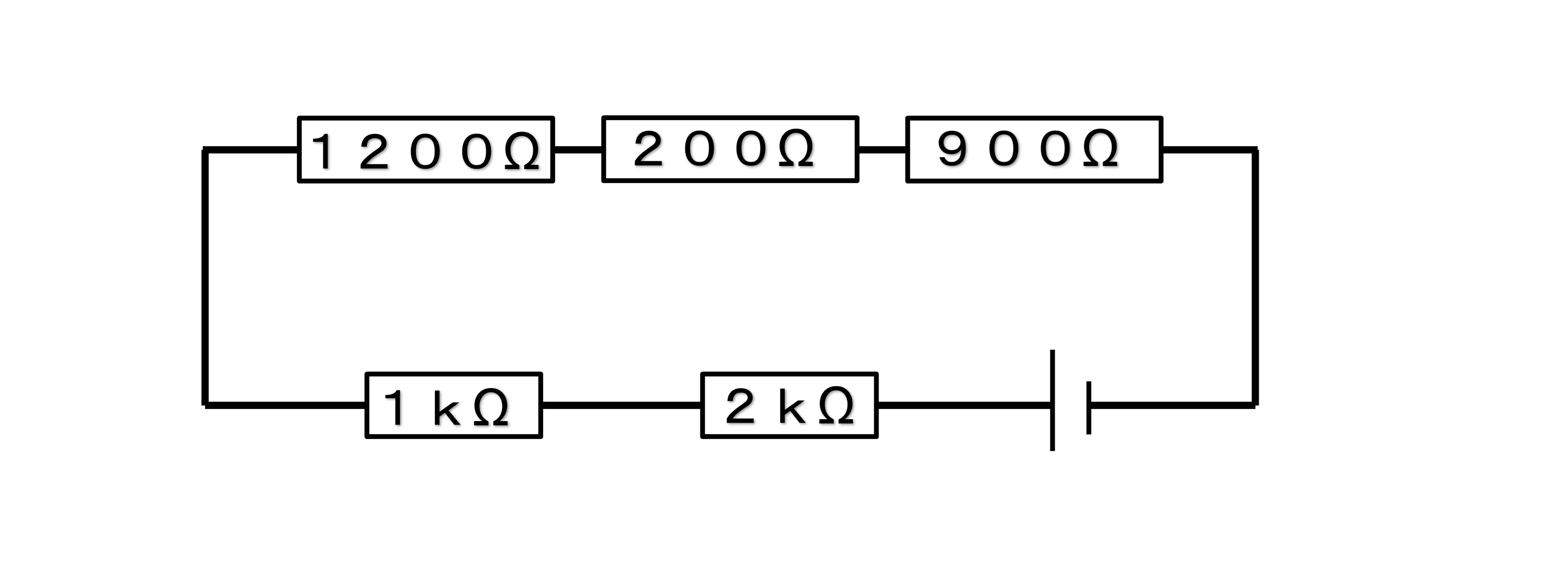
抵抗が直列につながれている場合と同じ状況なので、各抵抗の和で求めることができます。
2(kΩ)+1(kΩ)+1200(Ω)+200(Ω)+900(Ω)
=2(kΩ)+1(kΩ)+1.2(kΩ)+0.2(kΩ)+0.9(kΩ)
=5.3(kΩ)
A.5.3kΩ
まとめ
合成抵抗の「抵抗が並列に並んでいる場合」は都立高校の理科の入試問題でも、あまり出題されない分野です。
今回紹介した内容は、難易度が非常に高く、すべての学校で出題されるものではありません。
学校の授業をしっかりと聞いて、どこまでの知識が求められるのかを把握した上で勉強をしてください。
実技の基本は授業内にあります。
もし自分だけでは難しければ、東都ゼミナールではテスト前に各学校ごとに実技の対策も行っています。
実技の評定は都立高校の入試では2倍になるため考えようによっては英語や数学よりも重要です。
9科目全部の対策なら東都ゼミナールにお任せください。











